How to make a Stereo Camera Rig without Maya 2009
This page is not intended as a tutorial: it is only a guideline for implementing a stereo camera rig, when the tools offered by the latest release of Maya are not available.
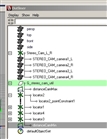
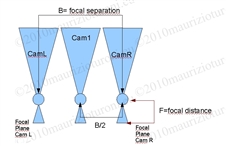
I utilise a file with 4 cameras (but you can use just two), symmetrical on the x axes from the centre named, for example " whatever_cam1_L" and "whatever_cam3_L" for the left cameras, "whatever_cam2_R" and "whatever_cam4_R" for the right ones. Linking from the left to the right camera, with point-constraints between the cameras on the distance dimension (from camera L to camera R) will formulate the camera separation.
These cameras become offset from a locator place in the center (0,0,0) called "Stereo_Cam_L_R", so that the camera can slide along the local axis X. This file is placed in available memory, named as StereoCamere, and will be imported into the scene. In Picture1 the Maya Outliner's file
At this point we can open the scene file that we want to make stereo. The donkey work is performed by a python script, loading the camera file into the scene, adding the camera stereo rig, as follows:
1. Import the StereoCamere file.
2. Determine the main camera's position and rotation in the scene, in this case Camera1. Create a parent constaint from the main camera to Stereo_Cam_L_R, the locator that is the parent of the stereo cameras.
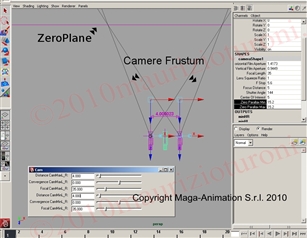
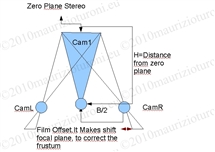
3. Make a plane (named O_zpn) with no render options; this will be the zero plane, placed in front of camera1 and assigned the same position and rotation as camera 1.
4. Create a locator (named Loc_zpn) with the same position and rotation as camera 1.
5. Create a Parent constraint on the Loc_zpn that will be attached to camera1.
6. Make O_zpn the child of Loc_zpn.
7. Add two scale attributes (or just one if you only have two cameras) to the camera shape, setting the distance from camera1 to the plane which is missing stereo.
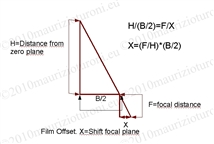
8. The most important point of the process: a script generates a
formula that calcultes correctly the attribute for the stereo
camera's Film Offset attribute, ensuring the correct convergence of
the two frustum cameras on the plane zero. See PICTURE on right.
The formula allows the convergence of the frustum stereo cameras, using
the 'Film offset' attribute, and calculates the coefficient necessary
utilising the law for triangle similarity.